Pola Bilangan Dan Rumus Un dari Pola Bilangan adalah sebuah barisan bilangan yang membentuk pola tertentu sehingga dapat diperoleh rumus umum untuk menentukan suku ke – n dari suatu pola bilangan. Terdapat beberapa pola bilangan yang perlu sobat idschool ketahui. Apa saja pola bilangan itu? Bagaimana rumus Un dari pola bilangan dan apa apa manfaat rumus Un? Melalui halaman ini, sobat idschool dapat mempelajarinya.

Simak lebih lanjut pembahasan pola bilangan dan rumus Un dari pola suatu pola bilangan pada masing – masing bahasan di bawah.
Pola Bilangan Ganjil
Pola bilangan ganjil adalah barisan loncat yang terdiri atas kumpulan bilangan ganjil. Barisan bilangan yang merupakan pola bilangan ganjil adalah 1, 3, 5, 7, dan seterusnya. Rumus Un untuk pola bilangan ganjil dan bentuk pola bilangan ganjil dapat dilihat seperti berikut.
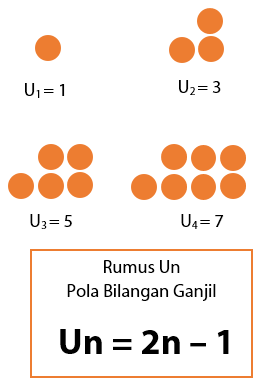
Pola Bilangan Genap
Hampir sama seperti pola bilangan ganjil, pada pola bilangan genap juga merupakan barisan bilangan loncat yang merupakan kumpulan bilangan genap. Contoh pola bilangan genap: 2, 4, 6, 8, dan seterusnya. Rumus Un pola bilangan genap dan bentuk pola bilangan genap diberikan seperti berikut.
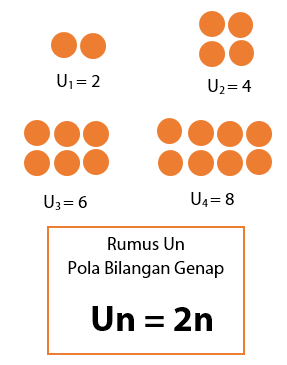
Pola Bilangan Segitiga
Pada pola bilangan segitiga, barisan bilangan yang mewakili bundaran yang dapat membentuk segitiga. Contoh pola bilangan segitiga: 1, 3, 6, 10, dan seterusnya. Rumus Un pola bilangan segitiga dan bentuk pola bilangan segitiga diberikan seperti gambar di bawah.
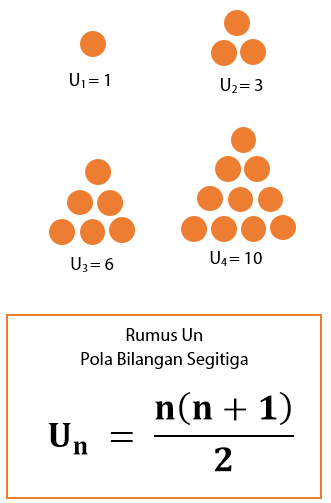
Pola Bilangan Persegi
Untuk pola bilangan persegi memiliki pola yang sama dengan pola bilangan pangkat dua. Barisan bilangan yang menyusun pola bilangan persegi juga merupakan pola bilangan pangkat dua. Sehingga rumus Un pola bilangan persegi dapat dinyatakan sebagai pangkat dua dari suatu bilangan. Contoh pola bilangan persegi: 2, 4, 9, 16, dan seterusnya.
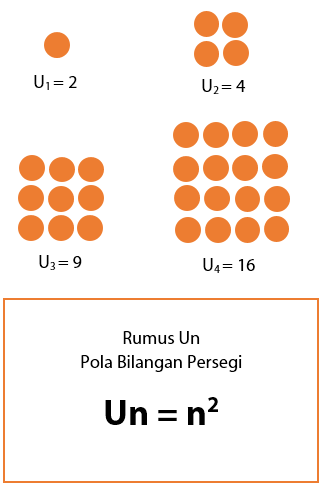
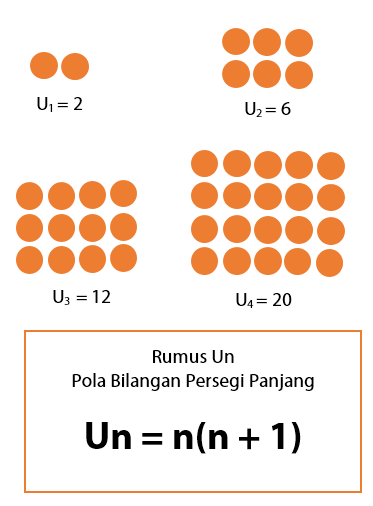
Pola Bilangan Persegi Panjang
Contoh pola bilangan persegi panjang: 2, 6, 12, 20, dan seterusnya. Rumus Un untuk pola bilangan persegi dapat dinyatakan melalui rumus Un = n(n + 1). Bentuk pola bilangan persegi panjang dapat dilihat pada gambar berikut.
Pola Bilangan Segitiga Pascal
Pola bilangan segitiga pascal merupakan jumlah bilangan – bilangan dari setiap baris pada segitiga pascal. Contoh pada baris ke 4 dari segitiga pascal terdiri atas barisan bilangan 1, 2, dan 1 sehingga bilangan U4 sama dengan 1 + 2 + 1 = 4. Barisan bilangan segitiga pascal adalah 1, 2, 4, 8, 16, 32, dan seterusnya.
Bentuk pola bilangan segitiga pascal dapat dilihat pada gambar berikut.

Pola Bilangan Fibonacci
Pola bilangan Fibonacci diperoleh dari menjumlah dua bilangan sebelumnya. Secara sederhana, rumus Un pola bilangan Fibonacci dinyatakan melalui rumus Un = Un – 1 + Un – 2. Contoh barisan bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, dan seterusnya.

Pola Bilangan Berpangkat
Polan bilangan berpangkat merupakan barisan bilangan dari bilangan pangkat, baik pangkat dua, pangkat tiga, atau pangkat untuk bilangan yang lebih besar. Contoh bilangan pangkat dua adalah 1, 4, 9, 16, 25, dan seterusnya. Sedangkan pola bilangan pangkat 3 adalah 1, 8, 27, 64, 125, dan seterusnya.

Pola Bilangan Aritmatika
Pola bilangan Aritmatika adalah barisan bilangan yang memiliki beda yang sama untuk setiap kenaikan sukunya. Contoh bilangan aritmatika adalah 1, 5, 9, 13, 17, dan seterusnya. Di mana barisan bilangan tersebut memiliki nilai beda sama dengan 4 (empat) untuk setiap kenaikan sukunya.
Secara umum, bentuk pola bilangan aritmatika dan rumus Un (suku ke – n) pada bilangan aritmatika diberikan seperti berikut.

Pola Bilangan Geometri
Pola bilangan geometri adalah barisan bilangan yang memiliki rasio yang sama untuk setiap kenaikan sukunya. Contoh pola bilangan aritmatika terdapat pada barisan bilangan 3, 6, 12, 24, dan seterusnya. Di mana barisan bilangan tersebut memiliki nilai rasio sama dengan 2 (dua) untuk setiap kenaikan sukunya.
Berikut ini gambaran pola bilangan geometri beserta rumus Un pola bilangan geometri.

Tidak ada komentar:
Posting Komentar